Innovation et prise de décision

En innovation, il est primordial de prendre les bonnes décisions. Pour ce faire, les entreprises modernes se basent habituellement sur leur intelligence d’affaires.  Il faut toutefois savoir que "la prise de décision ne doit pas uniquement se faire sur la vélocité de l’information en intelligence d’affaires, elle doit aussi être en étroite relation avec la compréhension de l’impact des décisions sur la performance dans le temps."[i]

Afin d’en arriver à cette compréhension, j’aimerais vous parler des modèles de simulation.  "Ceux-ci permettent de contribuer à un meilleur contrôle des risques et à une prise de décision beaucoup plus efficace en présence d’incertitude."[ii]

Il existe plusieurs types d’outils pour nous aider à bâtir des modèles de simulation :

Harvard Business Review[iii]

• "Les outils classiques de budgétisation des investissements; Ces outils estiment la progression de la marge bénéficiaire d’un projet, selon le potentiel d’investissement, pour établir s’il est avantageux d’y investir.
• Les outils d’analyses qualitatives; Permettre la prise de décisions en fonction d’un ensemble de scénarios qualitatifs représentant comment le présent pourrait évoluer dans le futur et en identifiant les conséquences des décisions considérées.
• Les outils de scénarios quantitatifs; Ces outils analysent les décisions en spécifiant les résultats possibles et leurs probabilités.  Ils utilisent des méthodes mathématiques, statistiques et de simulation pour identifier les risques et bénéfices potentiels de nos choix.
• Les outils de raisonnement basé sur des cas; Une approche méthodique qui permet la synthèse des informations recueillies dans les expériences passées qui sont similaires à celle recherchée afin d’aider dans la prise de décision.
• Les outils de recoupement d’informations; Il s’agit de collecter et de compiler l’information de diverses sources afin d’aider dans la prise de décision."[iii]

Powersim - Cloutier(2013)

Pour illustrer mon propos, je m’inspire d’un exemple que j’apprécie particulièrement, soit le calcul du taux d’adoption des technologies, proposé par Martin Cloutier Ph.D., dans le cadre de son cours "Technologies de la décision et système d'information - MBA UQAM 2013".  Dans ce cas précis, le choix de modèle de simulation est le scénario quantitatif.  L’outil que je recommande pour ce modèle est Powersim, maintenant partenaire avec la compagnie SAP [iv].

Cependant, il peut être très complexe de comprendre un modèle quantitatif, sans connaitre le raisonnement et les formules derrière son développement.  C’est pourquoi dans cet article, je vous propose une représentation à l’aide d’un modèle d’analyses qualitatives.  L’outil, ou plus précisément la méthode, que j’utilise est le diagramme d’influence (DI) [v].  Avec le DI que voici, vous aurez une représentation concise du schéma mental du modèle.  Ce schéma vous aidera à mieux comprendre le taux d’adoption de nouvelle technologie.

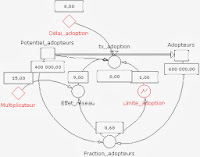
Diagramme d'Influence du Taux d'Adoption des Technologies

Description des éléments (variables et constantes du modèle) :

• Les éléments exogènes (externe au modèle) : Il y en a deux, ce sont des constantes, le Délai d’adoption et le Multiplicateur.
• Les éléments endogènes (interne au modèle) : Il y en a six.  Les deux premiers sont des variables de niveau, le Potentiel d’adopteurs et les Adopteurs.  Le troisième est une variable de taux, Taux d’adoption, calculé de la façon suivante : Potentiel d’adopteur * Effet réseau * (1 – Limite adoption) / Délai adoption.  Les trois derniers sont des variables auxiliaires. La Fraction d’adopteurs (égale à Adopteurs / (Adopteurs + Potentiel d’adopteurs)), la Limite d’adoption (qui est un graphique représentant une courbe croissante de 0 à 1 (axe des Y) avec un axe des X variant selon la Fraction d’adopteurs) et l’Effet réseau (égal à Fraction d’adopteurs * Multiplicateur).

Description des boucles et relations :

• Il y a premièrement un équilibrage (E1) (nombre impair d’influences opposées) entre Potentiel d’adopteurs et Taux d’adoption. Cela s’explique, car plus le Potentiel d’adopteurs augmente (diminue), plus le Taux d’adoption augmentera (diminuera) aussi.  Par contre, à l’inverse, plus le Taux d’adoption augmente (diminue), plus le Potentiel d’adopteurs diminuera (augmentera).
• La deuxième boucle d’équilibrage (E2) s’explique, car plus le Taux d’adoption augmente (diminue), plus le nombre d’Adopteurs augmentera (diminuera), plus la Fraction d’adopteur augmentera (diminuera) et plus la Limite d’adoption augmentera (diminuera) aussi. Finalement, à l’inverse, plus la Limite d’adoption augmentera (diminuera) et plus le Taux d’adoption diminuera (augmentera).
• La troisième boucle d‘équilibrage (E3) s’explique, car plus le Taux d’adoption augmente (diminue) et plus, à l’inverse, le Potentiel d’adopteurs diminuera (augmentera) et plus la Fraction d’adopteurs diminuera (augmentera). Par contre, plus la Fraction d’adopteurs augmente (diminue) et plus la Limite d’adoption augmentera (diminuera) aussi.  Finalement, comme nous le savons déjà, il y a influence opposée entre la Limite d’adoption et le Taux d’adoption.
• Il y a aussi deux boucles de renforcements (nombre pair d’influences opposées).  La première (R1), s’explique car plus le Taux d’adoption augmente (diminue) et plus le nombre d’Adopteurs augmentera (diminuera), plus la Fraction d’adopteur augmentera (diminuera), plus l’Effet réseau augmentera (diminuera) et plus le Taux d’adoption augmentera (diminuera) aussi.
• La dernière boucle, de renforcement aussi, s’explique, car il y a une influence opposée entre le Taux d’adoption, le Potentiel d’adopteurs et la Fraction d’adopteurs. Elle s’explique aussi, parce qu’il y a une Influence positive entre la Fraction d’adopteurs, l’Effet réseau et le Taux d’adoption.

Ce modèle n’est pas nécessairement complet, mais il vous explique clairement les fondements du taux d’adoption des innovations de nouvelles technologies.  Selon vous, quels autres éléments devrions-nous ajouter pour améliorer le modèle?

Si vous êtes gestionnaire, savoir quand décider est aussi important que de savoir quoi décider.  Les modèles de simulations sont de bons outils pour vous aider dans cette quête.  En tant que gestionnaire, il est donc important de bien connaître ces outils et de bien les utiliser lors des décisions importantes.  Maintenant, posez-vous la question...  Est-ce que votre organisation utilise des modèles de simulations pour la prise de décision?

---

[i] L. Martin Cloutier, Université du Québec à Montréal, and Centre de recherche en gestion, Méthodes pour dégager les données pertinentes: l’information en soutien à la prise de décision (Montréal: Université du Québec à Montréal, Centre de recherche en gestion, 2001).

[ii] Frank Hyneman Knight, Risk, Uncertainty and Profit (Cosimo, Inc., 2005).

[iii] Hugh Courtney, Dan Lovallo, and Carmina Clarke, “Deciding How to Decide,” Harvard Business Review Magazine, November 2013.

[iv] “SAP Software Partner,” October 2007, http://www.powersim.com/info/about/press-releases/sap-software-partner2/.

[v] Martin Cloutier, “L’information simulée en soutien à la prise de décision: Concepts et applications en financement d’entreprises” (Québec, 2002).

Un département d’innovations – Partie 2

À la suite de mon dernier article Un département d’innovations – Partie 1, j’ai fait la lecture de plusieurs articles et de deux ouvrages sur DARPA, que voici :

• The Department of Mad Scientists: How DARPA Is Remaking Our World, from the Internet to Artificial Limbs[i]
• Cloning DARPA Successfully[ii]

Pour vous permettre de cloner DARPA efficacement, je propose donc une brève analyse desdits comportements organisationnels chez DARPA, selon les théories expliquées dans l’ouvrage « Comportement Organisationnel – Comportements humains et organisations dans un environnement complexe »[iii] :

• Les personnalités dominantes des employés, selon la théorie du Big Five, sont la fiabilité et l’ouverture à l’expérimentation.  Selon la théorie MBTI (Myers-Briggs), on les catégorise comme personnalité adaptative et à haut besoin d’accomplissement.

• La motivation des individus passe par la responsabilisation, la nature du travail et l’accomplissement. Ce sont les facteurs de satisfaction dominants, selon la théorie de Herzberg, qui permettent aux employés de DARPA de garder un haut degré de productivité.  Une autre théorie qui s’applique est celle des attentes (Vroom) : les individus croient que leurs efforts les conduiront à atteindre un certain niveau de performance, elle-même source de résultats ou de récompenses qu’ils valorisent.[iv]

• L’autonomie, l’agilité et la simplicité (minimalisation de la bureaucratie) des équipes de travail sont primordiales pour l’atteinte des objectifs.  Il s’agit donc d’une structure organisationnelle "divisionnalisée" avec des équipes de travail autonomes :
• Pour rassembler le personnel autour d’un même projet d’innovation et
• Pour effectuer un travail complet comprenant plusieurs tâches interdépendantes, tout en jouissant d’une grande autonomie dans l’exécution de leur travail.[v]

• Un processus décisionnel et de pouvoir centralisé aux chefs de projets : contrairement à ce que l’on pourrait croire, les décisions ne se font pas en groupe, car les innovations n’ont pas tendance à faire consensus[vi].  Il est donc primordial d’avoir un chef très fort, très instruit, capable de faire des choix difficiles, de prendre des risques et de savoir recruter des ressources de très haut calibre.

• Aménagement de travail efficace pour une communication optimale : primordial dans un contexte d’innovation, l’information doit circuler librement à tous les niveaux d’une équipe de projets.

• Des contrôles de gestion privilégiant la créativité et la flexibilité : les gestionnaires vont surveiller si les objectifs sont atteints sans fournir des façons de procéder préétablies. C’est pourquoi chez DARPA, les chefs de projet font une gestion baladeuse, c’est-à-dire qu’ils sortent de leurs bureaux pour glaner de l’information au cours d’échanges informels avec les employés.[vii]

• Leadership orienté vers les résultats : il s’agit d’une théorie de l’adéquation chemins-buts[viii] ou les comportements du chef encouragent les employés à atteindre des performances élevées. 

• Une culture organisationnelle avec forte tendance à innover et à prendre des risques.

Mon analyse sur DARPA, sans être scientifique, apporte un éclairage sur les comportements organisationnels que vous devriez adopter, dans l’éventualité où vous envisageriez le déploiement d’un département d’innovation dans votre organisation. 

Il importe cependant, avant de vous lancer dans une aventure de cette envergure, de bien vous questionner sur les risques financiers associés à un département d’innovation.

Votre organisation est-elle prête ou simplement capable de les assumer ?

---

[i] Michael P Belfiore, The Department of Mad Scientists: How DARPA Is Remaking Our World, from the Internet to Artificial Limbs (New York: Harper, 2010).

[ii] Erica R.H. Fuchs, “Cloning DARPA Successfully: Those Attempting to Copy the Agency’s Success in Advancing Technology Development First Better Be Sure They Know How DARPA Actually Works (Defense Advanced Research Projects Agency ),” Science and Technology, September 22, 2009.

[iii] Charles Benabou, Steven McShane, and Sandra L. Steen, Comportement organisationnel : Comportements humains et organisations dans un environnement complexe, 2e édition (Canada: Chenelière, 2013).

[iv] Victor Harold Vroom, Work and Motivation (New-York: John Wiley & Sons, 1967).

[v] Susan Albers Mohrman et al., Designing Team-based Organizations: New Forms for Knowledge Work (États-Unis: Jossey-Bass, 1995).

[vi] Regina E. Dugan and Kaigham J. Gabriel, “‘Special Forces’ Innovation: How DARPA Attacks Problems,” HBR - The Magazine, October 2013, http://hbr.org/2013/10/special-forces-innovation-how-darpa-attacks-problems/ar/1.

[vii] Thomas J. Peters and Robert H. Waterman, In Search of Excellence: Lessons from America’s Best-Run Companies (UK: HarperCollins, 2004).

[viii] Robert J. House, “Path-goal Theory of Leadership: Lessons, Legacy, and a Reformulated Theory,” The Leadership Quarterly 7, no. 3 (1996): 323–352, doi:10.1016/S1048-9843(96)90024-7.